분할 상환 분석은 연산을 번 했을 때 총 드는 시간 를 으로 나눠주는 “할부” 개념이라고 배웠는데요. 최악의 경우로 시간 복잡도를 얘기하는 것이 비합리적인 경우에 사용하죠. 이번 레슨에서는 동적 배열의 추가(append) 연산에 직접 분할 상환 분석을 해 봅시다.
동적 배열 동작
동적 배열에 추가를 할 때는:
- 새로운 인덱스에 데이터를 저장하는 시간
- 기존 배열의 크기가 부족해서 더 큰 배열을 만들고, 기존 배열의 데이터들을 옮기는 시간
이 두 가지를 나눠서 생각하면 편합니다.
우선 기억을 상기시키기 위해서 동적 배열에 데이터를 추가할 때 일어나는 일들을 쭉 나열해 볼게요.
비어 있는 동적 배열에 추가 연산을 9번 한다고 가정합시다. 처음 시작할 때 동적 배열은 크기가 1인 배열입니다.
- 첫 번째 요소 추가:
- 그냥 새로운 데이터를 저장합니다.
- 두 번째 요소 추가:
- 배열이 꽉 찼습니다. 크기가 2인 배열을 새로 만들고 기존 데이터를 옮겨 저장합니다 (1 개 옮겨 저장)
- 맨 뒤 인덱스에 새로운 데이터를 저장합니다.
- 세 번째 요소 추가:
- 배열이 꽉 찼습니다. 크기가 4인 배열을 새로 만들고 기존 데이터를 옮겨 저장합니다 (2 개 옮겨 저장)
- 맨 뒤 인덱스에 새로운 데이터를 저장합니다.
- 네 번째 요소 추가
- 맨 뒤 인덱스에 새로운 데이터를 저장합니다.
- 다섯 번째 요소 추가
- 배열이 꽉 찼습니다. 크기가 8인 배열을 새로 만들고 기존 데이터를 옮겨 저장합니다 (4 개 옮겨 저장)
- 맨 뒤 인덱스에 새로운 데이터를 저장합니다.
- 여섯 번째 요소 추가
- 맨 뒤 인덱스에 새로운 데이터를 저장합니다.
- 일곱 번째 요소 추가
- 맨 뒤 인덱스에 새로운 데이터를 저장합니다.
- 여덟 번째 요소 추가
- 맨 뒤 인덱스에 새로운 데이터를 저장합니다.
- 아홉 번째 요소 추가
- 배열이 꽉 찼습니다. 크기가 16인 배열을 새로만들고 기존 데이터를 옮겨 저장합니다 (8 개 옮겨 저장)
- 맨 뒤 인덱스에 새로운 데이터를 저장합니다.
이런 식으로 내부 배열이 꽉 찼을 때는 새로운 배열을 만들고, 기존 요소들을 복사하고, 새로운 요소를 저장하면 됩니다. 그리고 배열에 여유가 있으면 그냥 새로운 요소만 저장하면 되죠?
분할 상환 분석
분할 상환 분석을 하면 이 동작을 번 반복한다고 가정합니다. 총 걸리는 시간을 계산하기 쉽게 두 가지로 나눠서 생각해 볼 거라고 했잖아요?
- 새로운 데이터를 동적 배열 맨 끝에 단순히 저장하는 데 걸리는 시간
- 더 큰 배열을 만들고 그 배열에 기존의 데이터를 옮기는 데 걸리는 시간
걸리는 두 시간을 각각 따로 계산해 볼게요.
배열 끝에 새로운 데이터 저장하는 데 걸리는 시간
먼저 새로운 데이터를 저장하는 데 걸리는 총 시간에 대해서 생각해 봅시다.
| x번째 추가 | 배열 끝에 데이터 저장하는 데 걸리는 시간 |
| 1 | 1 |
| 2 | 1 |
| 3 | 1 |
| 4 | 1 |
| 5 | 1 |
| 6 | 1 |
| 7 | 1 |
| 8 | 1 |
| 9 | 1 |
| … | 1 |
| 1 |
인덱스에 데이터를 저장하는 데 걸리는 시간은 1이라고 했잖아요? 이걸 총 번 하는 거니까 이 걸리겠죠?
새로운 배열에 데이터 옮기는 시간
이번에는 내부 배열이 꽉 차서 기존 데이터를 복사하는 데 걸리는 시간에 대해서 생각해 봅시다. 이 부분이 좀 어려우니까 집중해서 보세요.
| x 번째 추가 | 배열 크기 | 새로운 배열에 요소 옮겨 저장하는 데 걸린 시간 |
| 1 | 1 | 0 |
| 2 | 2 | 1 |
| 3 | 4 | 2 |
| 4 | 4 | 0 |
| 5 | 8 | 4 |
| 6 | 8 | 0 |
| 7 | 8 | 0 |
| 8 | 8 | 0 |
| 9 | 16 | 8 |
| … | 0 | |
| n |
새로운 배열에 기존 데이터를 옮겨 저장하는 시간은 위 표에 나와 있는대로 소요됩니다.
표를 살펴봅시다. 2 번째, 3 번째, 5 번째, 9 번째 추가 때 배열의 크기를 늘려야 합니다. 그럴 때마다 데이터를 옮겨야 하는데요. 이때 데이터를 각각 1, 2, 4, 8 개씩 복사하고 붙여 넣습니다.
데이터를 복사해서 붙여 넣는 총 시간 비용은 이 시간들을 더한 인데요. 좀 더 일반화해서 생각할까요?
추가 연산을 번 했을 때, 가장 마지막에 데이터를 m개 옮겨서 저장했다고 합시다.
그럼 데이터를 복사해서 저장하는 데 걸린 총 시간은 : m 이렇게 표현할 수 있는데요. 이걸 도형으로 나타내 볼게요. 이런 식으로 처음에 이 있고 그 다음에 계속 반으로 줄어든 값을 더해 주겠죠?
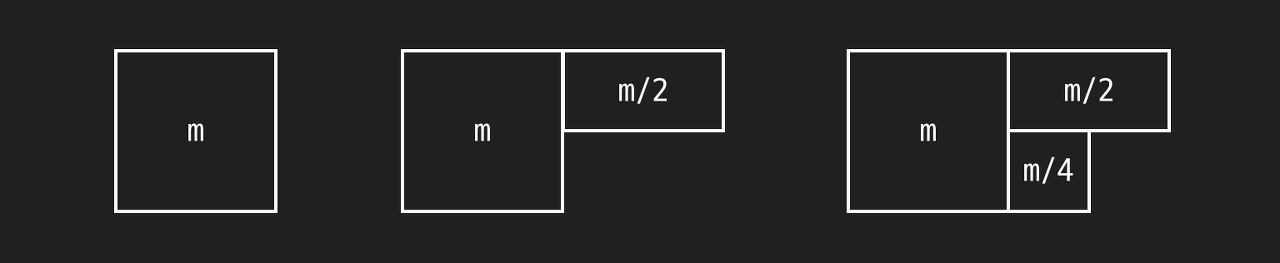
처음에 이렇게 더해 주다가, 결국에는 이렇게 될 텐데요.

도형에서 볼 수 있듯이 이런 식으로 어느 자연수든 반씩 줄여서 1까지 계속 더해주면 그 결과는 절대 2�을 넘을 수 없습니다. 정확히 말하면 딱 이 되죠.
근데 가장 최근에 데이터를 옮겨 저장할 때 8이 걸렸다는 건 무슨 의미일까요? 원래 배열의 수용 가능 크기가 8이었지만 크기가 부족해서 16개의 데이터를 담을 수 있는 새로운 배열로 복사했다는 얘기인데요. 그럼 결국에 현재 배열 안에 있는 데이터는 9개에서 16개 사이라는 말입니다. 16개보다 더 많은 요소가 있으면 가장 최근에 옮겨 저장한 요소의 수가 8이 아니라 16이겠죠?
이 사실을 바탕으로 우리가 일반화할 때 사용했던 배열 안 요소 수 과 가장 최근 옮겨 저장한 요소 수 의 관계에 대해서 한 가지 사실을 알아낼 수 있는데요.
가장 최근에 복사하는 데 걸린 시간이 8일 때, 배열 안에 있는 데이터는 9개에서 16개 사이입니다. 즉, 은 무조건 보다 작다고 할 수 있습니다.
추가 연산을 연속으로 번 하고, 가장 마지막에 옮겨 저장한 데이터 요소 수를 이라고 할 때:
- 복사해서 저장하는 데 걸리는 총 시간이 이고
- 은 보다 작습니다.
이걸 다시 정리해서 나타내면:
연속으로 추가 연산을 � 번을 하면 데이터를 옮겨서 저장하는 데 걸리는 총 시간은 2� 보다 작다!
라고 할 수 있습니다.
두 경우 합치기
지금까지 나온 내용을 종합해 보면, 동적 배열에 개의 데이터를 연속으로 추가하면:
- 새로운 데이터를 저장하는 데에는 의 시간이 들고,
- 데이터를 옮겨 저장하는 데에는 2보다 적은 시간이 걸리는데요.
이 두 시간을 합치면 총 드는 시간은 보다 적은 시간이 걸리겠죠? 이걸 시간 복잡도로 표현하면 , 그러니까 이라고 할 수 있습니다.
근데 이건 추가 연산을 한 번 하는 게 아니라 연속으로 번 하는 데 걸리는 시간 복잡도입니다.
그러니까 총 번의 추가 연산을 하는 데 걸리는 시간이 인 건데요. 추가 연산을 번 하는 데 의 시간이 걸리니까 1 번 하는 데는 , 즉 이 걸리는 거죠.
전에는 추가 연산이 최악의 경우 이 걸린다고 했었는데요. 분할 상환 분석을 하면 이 걸린다고 보는 거죠.
최악의 경우 분석 vs. 분할 상환 분석 뭘 쓰면 되는 걸까
사실 분할 상환 분석을 한다고 꼭 시간 복잡도가 줄어드는 건 아닙니다. 보통은 할부 개념을 적용해도 시간 복잡도가 줄어들지 않죠.
하지만 만약 최악의 경우보다 분할 상환 분석을 한 시간 복잡도가 더 적다면, 분할 상환 분석을 한 시간 복잡도를 사용합니다. 그러니까 “동적 배열의 끝에 데이터를 추가할 때는 이 걸린다.”라고 표현해도 된다는 거죠.
보통은 혼란을 없애기 위해 좀 더 정확하게:
동적 배열의 추가(append) 연산은 최악의 경우 이 걸리지만, 분할 상환 분석을 하면 이 걸린다.
라고 표현할 수 있습니다!
'Algorithm > 자료구조' 카테고리의 다른 글
| [링크드 리스트] 링크드 리스트 __str__ 메소드 (0) | 2023.07.31 |
|---|---|
| [배열] 동적 배열 크기 줄이기 (0) | 2023.07.31 |
| [배열] 동적 배열 삭제 연산 (0) | 2023.07.31 |
| [배열] 파이썬 리스트(동적 배열)의 비밀 (0) | 2023.07.28 |
| [기본 자료 구조] 데이터의 주소 (0) | 2023.07.27 |
